Control of nanoparticles with arbitrary 2-D force fields (with W. E. Moerner, Stanford)
Under normal operation the ABEL trap provides a feedback electric field proportional to the most recently measured offset of the particle from the target location, and pointing back toward the target. However, it is simple to apply feedback using more complicated rules as well. The feedback voltage can be an arbitrary function of the present position of the particle, as well as its velocity, acceleration, or past positions. Furthermore, because we specify the force field and not the potential, there is no requirement that the force field be conservative. Thus the ABEL trap provides a platform for observing Brownian dynamics subject to complex force fields.
 |
We investigated the motion of fluorescent polystyrene nanospheres subject to power law force fields of the form:
when b = 1, this corresponds to a linear restoring force, or a parabolic potential. We investigated potentials between b = 4 and b = -1 (the limit of stability). We found that the probability density function in a power law potential was well described by a Boltzmann distribution. The figure shows the measured radial probability densities, the predictions of the Boltzmann distribution, and the results of a numerical simulation that took into account the finite latency of the feedback in the trap. Only with sharply kinked potentials (0 > b > -1) was there a deviation. This deviation was due to the finite latency of the feedback, as shown by numerical simulations (green curves). |
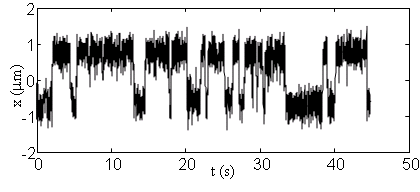
| We also looked at force fields corresponding to a double well potential: |
 |
| The hopping rate between minima was as predicted by Kramers' theory. The figure shows a typical trajectory: |
 |
Documentation:
- Adam Cohen: Control of nanoparticles with arbitrary two-dimensional force fields, Phys. Rev. Lett., 94, 118102, Mar. 25 2005
Press:
-
PRL Focus: Hold still, 22 March 2005