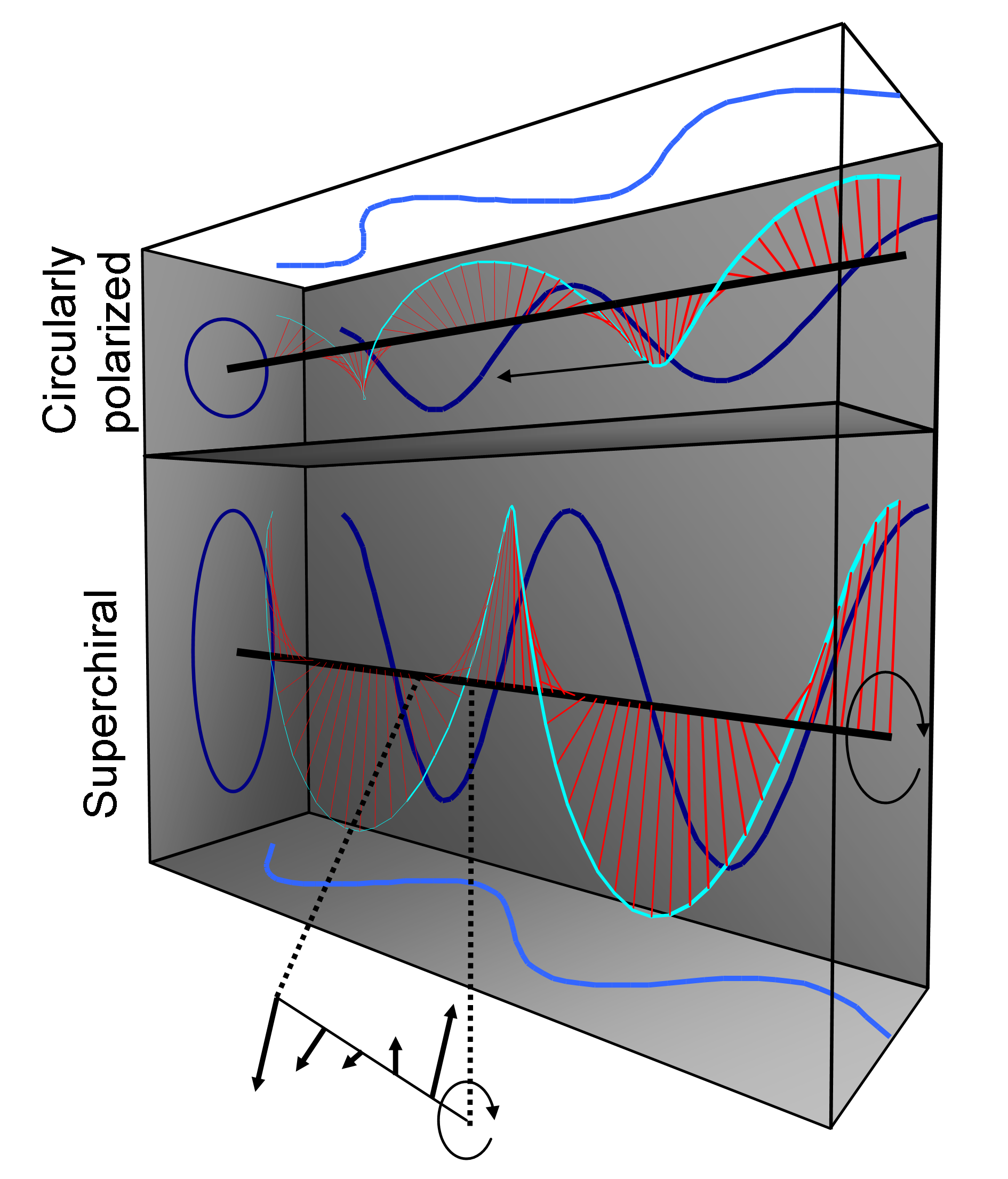
Optical Chirality and Its Interaction with Matter
We are working on a new class of spectroscopies in which the 3-dimensional shape of the electromagnetic field is engineered to induce qualitatively new physical effects in molecules. By sculpting the electromagnetic field we hope to photoexcite molecules of a single chirality in the presence of an excess of their mirror-image cousins, with enantioselectivity up to 100 times larger than is achieved by circularly polarized light.
It has long been known that chiral objects interact asymmetrically with chiral fields. For example, a chiral molecule is excited at slightly different rates when exposed to left- or right-circularly polarized light (CPL), an effect called circular dichroism. Circular dichroism (CD) is widely used to characterize organic and biological compounds.
Chiroptical effects are typically very small, because the wavelength of light is so much larger than the size of most molecules. The electromagnetic field undergoes a nearly imperceptible twist over molecular dimensions. To couple more strongly to molecular chirality, one should increase the chirality, or twistiness, of the electromagnetic field.
Optical Chirality
How does one measure the local chirality of the electromagnetic field? Any such measure should be a time-even pseudoscalar, i.e. it should associate a number to each position in the field, and this number should be opposite sign between mirror-image fields. None of standard measures of electromagnetic fields has the correct symmetry, so we made up a quantity which we call optical chirality. The table below shows the bilinear properties of the electromagnetic field, classified according to their symmetries.

In this table e0 and m0 are the permittivity and permeability of free space, E and B are the time-dependent electric and magnetic fields, and r is the position vector. Optical chirality is a fundamental property of the electromagnetic field, on an equal footing with energy density, linear momentum, and angular momentum. We generalized the theory of CD to include pairs of arbitrary mirror-image fields and found that the chiral bias in the light-matter interaction depends on both the molecular transition moments and optical chirality. By tuning optical chirality in a precisely sculpted electromagnetic field, nature may allow enhanced discrimination of chiral molecules against their mirror counterparts.
Superchiral light (SCL)
We found “superchiral” solutions to Maxwell’s Equations that show chiral asymmetries hundreds of times larger than the asymmetries of circularly polarized light, in small regions of space. The key is to set up an imperfect standing wave comprised of two counterpropagating CPL plane waves. The waves should have opposite handedness, the same frequency, and slightly different intensity. Enhancement in the chiral asymmetry is predicted at the nodes of the standing wave.
|
|
Experimental aspects
A superchiral standing wave is created simply by reflecting CPL of a single handedness off an imperfect mirror at normal incidence. The reflected wave and the incident wave combine to create a superchiral standing wave. Chiral molecules are confined to a nanometer-thickness film at a well-defined height above the mirror surface. Molecules positioned near a node in the superchiral standing wave are predicted to show enhanced chiroptical asymmetry.
|
|
The experimental setup enables fluorescence measurement to a fractional precision of 4 × 10-5. In the nodes of SCL, an 11-fold enhancement in enantioselectivity of exciting a thin film of chiral compound is observed. The experimental data coincide quantitatively with theoretical expectations.
|
intensity distribution in a superchiral standing wave. Superchiral nodes were identified by their correspondence with minima in the average fluorescence intensity. A.U., arbitrary units. (Insets) Images of the average fluorescence. B) Dissymmetry factor along a line cutting through a superchiral node in chiral (red) and achiral (orange) regions. Blue line marks the value of the position-independent dissymmetry factor measured in chiral films without superchiral enhancement. Black line is the theoretical prediction for the dissymmetry factor, calculated in. Error bars are SEM of 400 measurements. (Insets) Spatial maps of the dissymmetry factor near the superchiral nodes. |
Optical chirality is a fundamental and tunable property of light. Our demenstration of superchiral light raises exciting possibilities to sculpt the three-dimensional shape of the electromagnetic field, to bring other dark transitions to light.
|
|
-
Documentation:
- N. Yang, A. E. Cohen, Local geometry of electromagnetic fields and its role in molecular multipole transitions, J. Phys. Chem. B, 115, 5304-5311, 2011.
- Y. Tang, L. Sun, A. E. Cohen, Chiroptical hot spots in twisted nanowire plasmonic oscillators, Applied Physics Letters, 102, 043103, 2013. Supporting Information.
- Yiqiao Tang and Adam E. Cohen, Enhanced enantioselectivity in excitation of chiral molecules by superchiral light, Science, 332, 333, 2011
- Yiqiao Tang and Adam E. Cohen, Optical chirality and its interaction with matter, Physical Review Letters, 104, 163901, 2010.
- Yiqiao Tang, Timothy A. Cook and Adam E. Cohen, Limits on fluorescence detected circular dichroism of single helicene molecules, J. Phys. Chem. A, 113, 6213, 2009.
- Nan Yang, Yiqiao Tang and Adam E. Cohen, Spectroscopy in sculpted fields, Nano Today, 4, 269-279, 2009.
Supporting info and press:
- Supertwisty Light Proposed, Science News, April 10th, 2010; Vol.177 (p. 10)